|
Protokoll des 2. Treffens Nachdem wir uns bei unserem 1. Treffen mit den philosophischen und künstlerischen Aspekten des Zenonschen Paradoxons befasst haben, wollen wir uns eine Woche später mit dem mathematischen auseinandersetzen. Zuvor jedoch reflektieren wir noch einmal kurz das Problem des Bewegungsbegriffes. Dem zugrunde liegt das Bild "La Flèche de Zénon" (1964) René Magrittes. Der in der Bildmitte platzierte Stein ist als sinnbildliches Äquivalent zu Zenons Pfeil zu betrachten. Dieser ist in einem Standbild festgehalten, erstarrt also in einem Zeitpunkt, der über keinerlei Ausdehnung verfügt. Ohne Ausdehnung finden wir wiederum keine Bewegung vor, womit wir Zenons Standpunkt zulassen. Dieser erachtet Bewegung nämlich als inexistent, beschreibt sie stattdessen mit der kontinuierlichen Abfolge erstarrter Einzelbilder (Zeitpunkte), die uns die Illusion oktroyiert, es fände Bewegung statt. Somit widerspricht unsere sinnliche Erfahrung Zenon, die theoretische Herangehensweise jedoch vermag dies nicht. Ein Beispiel: Wir lassen einen Gegenstand auf den Boden fallen, genauso wie es sich mit Magrittes Stein auf seinem Bild verhält, respektive verhalten sollte. Was passiert mit unserer Wahrnehmung? Scheinbar beobachten wir den Weg des Objekts von Anfang bis Ende. Die sinnliche Erfassung dieses Vorgangs lässt uns einerseits daran glauben, andererseits spricht die Logik gegen diese Beobachtung der Bewegung. Wir haben es also mit einer interpretatorischen Sichtweise zu tun, die wir auch bei Magritte ansetzen, obwohl das Bild selbst ein starres ist. In geistiger Erzählung verfolgen wir den Weg weiter, den der Stein zu nehmen hat, so dass wir uns weitere Bilder erschaffen, die den Stein immer ein wenig weiter verschieben, dass wir letztlich einen Film (eine Bildfolge) abspielen. Was Zenon bewirkt, ist eine Auseinandersetzung mit der Wahrnehmung und das Infragestellen derselben, da sie scheinbar in häufigem Konflikt steht zur Wirklichkeit und ein teils antagonistisches Verhalten zu dieser aufweist. Andererseits müssen wir uns fragen, wie real die Wirklichkeit tatsächlich ist. Im Zenonschen Sinne ist sie unveränderlich und ewig, während Bewegung und Veränderung Illusion sind. (In diesem Kontext lässt sich der Film "Matrix" erwähnen.) Auch wenn sich die Frage nach Wirklichkeit und Illusion nie klären lässt, wollen wir ihr trotzdem nachgehen und noch einen Schritt weiter machen, nämlich hin zur Mathematik. Den mathematischen Aspekt haben wir bereits eingeführt, als wir uns mit Zenons Paradoxon des Wettlaufs zwischen Achilles und der Schildkröte befasst haben. Demnach kann Achilles die Schildkröte, der er einen Vorsprung gewährt, nie einholen, da er, obwohl er schneller ist, sich dieser zwar nähert, beim Durchlaufen der Strecke sich die Schildkröte selbst aber wieder einen (wenn auch kleineren) Vorsprung herausläuft. Hier haben wir die Zerteilung der Zeit in immer kleinere Abschnitte. Folgend beschäftigen wir uns eingehender mit der mathematischen Betrachtung des Phänomens der Bewegung, indem wir diese auch hier in immer kleiner werdende Abschnitte einteilen. Dazu gehen wir zunächst rein arithmetisch vor und ziehen zum abschließenden Grenzwertbegriff Zenon dazu. Wir wollen berechnen, welche Geschwindigkeit der Pfeil einnimmt, während er sich auf einem Punkt befindet, besser gesagt sich auf einem nicht mehr messbar kleinen Zeitabschnitt der Zeitachse bewegt. Auch in diesem Bereich aber muss sich der Pfeil bewegen, weil er sich insgesamt bewegt. Die allgemeine Formel für die Berechnung der Geschwindigkeit lautet |
|
|
|
|
|
In jedem Fall gilt der ungefähre Weg (s): s = 5t•t (hinreichende Näherung an diesen Wert) Für t wird ein Zeitabschnitt festgelegt, der sich aus t2 - t1 errechnet, so dass zur Ermittlung der Durchschnittsgeschwindigkeit (VD) folgende allgemeine Regel gilt: |
|
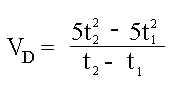 |
|
| Nun wollen wir die Momentangeschwindigkeit ermitteln, die Geschwindigkeit also, die nicht für einen Zeitabschnitt, sondern einen Zeitpunk gilt. Für t1 legen wir 1 sec. fest: | |
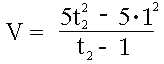 |
|
| Für t2 muss nun ein Wert gefunden werden, der annähernd an t1 heranreicht. Da dieser so klein wie möglich gehalten werden soll, setzen wir hierfür 1 + dt ein, wobei dt für eine Zahl steht, die größer als null, jedoch kleiner als die kleinste vorstellbar reelle Zahl ist - man nennt diese Zahlen infinitesimale Nicht-Standard-Zahlen (Newton sprich hierbei von Fluxionen, siehe weiter unten). Daraus ergibt sich: | |
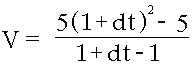 |
|
| Nach dem Lösen der binomischen Formel und dem Kürzen im Nenner sieht der Bruch wie folgt aus: | |
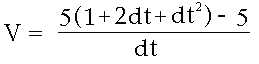 |
|
| Nun lösen wir die Klammer und kürzen: | |
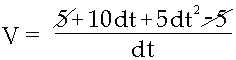 |
|
| Wir klammern dt aus: | |
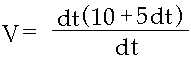 |
|
| Jetzt erst lassen wir Zenon zu. Wir bewegen uns immer noch in einem Zeitabschnitt, minimieren diesen aber immer weiter, indem wir einen Grenzwert bilden und dt gegen null laufen lassen: | |
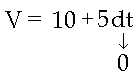 |
|
|
So stellen wir fest, dass die Momentangeschwindigkeit des Pfeils 10 m/sec. beträgt. Wir haben nun ein mathematisches Konstrukt (indem wir dt beliebig nahe dem Grenzwert 0 entgegenstreben lassen), dass mit der sinnlichen Erfahrung übereinstimmt. Zwar sind die errechneten 10 m/sec. sinnlich nicht erfahrbar, jedoch ist es die Gesamtgeschwindigkeit, die ein Objekt einnimmt. Abschließend muss man bemerken, dass zur Zeit Newtons der moderne Grenzwertbegriff noch nicht existierte. Newton hat sich stattdessen der Fluxionen (sein Begriff für Infinitesimale) angenommen, viele aneinandergereihte unendlich Teilbare, die den Bereich zwischen den kleinsten vorstellbar reellen Zahlen füllen. Laut Newton können wir somit den Wert dt beliebig nahe an 0 heranführen, diese jedoch nie erreichen, da immer ein Bereich übrigbleibe, der zwar nicht erfassbar aber dennoch vorhanden sei. 03.September 2001 : Alessandro Pesce Siehe auch |
|
|
Fahrtenwoche des 13. Jahrgangs |
|
|
"Mit dieser spektakulären Aufnahme, sie zeigt einen F-15-Kampfjet beim Durchbrechen der Schallmauer, gewann der Fotograf John Gay von der US-Zeitschrift "Sports Illustrated" beim diesjährigen Wettbewerb um das "World Press Photo" den ersten Preis in der Sparte Wissenschaft und Technik. Foto: dpa" Braunschweiger Zeitung 12.02.2000 |
 |
