|
|||||||||||
|
1.
- 3. Treffen | 4
.- 7. Treffen | 8. Treffen | 9. Treffen |
10. Treffen | 11.
Treffen | 12.-17.
TREFFEN | Anfang
|
|||||||||||
| HEINRICH-NORDHOFF-GESAMTSCHULE WOLFSBURG | KURSPROTOKOLL | ||||||||||
| MATHE+KUNST 13. Jahrgang GK 2001-02-1 |
7.
- 9. Stunde, Raum C 710
|
||||||||||
|
Birger
Sechtig & Rainer Randig
|
16.10.2001
|
||||||||||
|
Bild+Erläuterungen von Yasmin Schieweck Nach reichlichen Überlegungen
plante ich, einen Baum, dessen Krone vom Wind zu einer Seite gedrückt
wird, für die Aufgabe zu zeichnen. Das Paradoxe sollte die Umgebung,
die nicht vom Wind bewegt wird, widerspiegeln. |
|||||||||||
|
ich entschied mich ein Seil zu zeichnen,
welches straff in vertikaler Ebene gestreckt ist. Da ein Seil im ruhenden
Zustand schlaff herunter hängt und nur straff ist, wenn es festgehalten
und gedreht wird, ist mein Bild auf einer paradoxen Grundlage entstanden.
Hier sieht man weder eine Wie sind die anderen
Bilder entstanden? |
|||||||||||
|
Die Schüler sind auf unterschiedliche
Art und Weise an die Aufgabe herangegangen. Manche wussten sofort, wie
sie ihr Bild gestalten werden, andere wiederum sammelten erst viele
Ideen und wählten dann die ihnen am besten gefallende Idee aus. Hier ein paar Stichworte einer Schülerin
darüber, wie sie an diese Aufgabenstellung
|
Diese Ausführungen waren Bestandteil
der In den nächsten Stunden soll das Thema ZEIT noch weiter untersucht werden. |
||||||||||
|
1.
- 3. Treffen | 4
.- 7. Treffen | 8. Treffen | 9. Treffen | 10.
Treffen |
11.
Treffen | 12.-17.
TREFFEN | Anfang
|
|||||||||||
|
(S. nimmt an einer Fortbildungsveranstaltung teil) Zum Thema Zeit - Mensch
- Bildermachen - Kunst werden jeweils ein Ausschnitt aus dem Film
"An jedem verdammten Sonntag" (die letzten Minuten eines existentiell
wichtigen Footballspiels) und aus Kurosawas "Träume "
eingebracht. |
|||||||||||
|
1.
- 3. Treffen | 4
.- 7. Treffen | 8. Treffen |
9. Treffen | 10. Treffen | 11.
Treffen | 12.-17.
TREFFEN | Anfang
|
|||||||||||
|
(S. nimmt an
einem Symposion teil, R. krank) |
|||||||||||
|
1.
- 3. Treffen | 4.
- 7. Treffen | 8. Treffen | 9.
Treffen | 10.
Treffen| 11.
Treffen | 12.-17.
TREFFEN | Anfang
|
|||||||||||
|
Birger Sechtig:
|
 |
||||||||||
| Protokoll: Tina Barthel: | |||||||||||
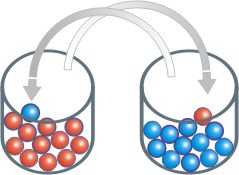
| Ist Zeit
unumkehrbar? Im ersten Teil unserer Unterrichtsstunde behandelten wir die Frage: Gibt es eine physikalische Tatsache, die den Zeitpfeil unumkehrbar macht? Diese Frage versuchten wir anhand eines Spieles zu beantworten. Bei diesem Spiel hatten wir zwei Tassen mit jeweils 30 roten und blauen Spielsteinen. Zu Beginn des Spiels sind in Tasse 1 nur rote und in Tasse 2 nur blaue Steine vorhanden. Nun begann eine Schülerin wahllos einen Stein aus Tasse 1 zu ziehen und diesen in Tasse 2 zu legen. Daraufhin zog sie aus Tasse 2 einen Spielstein und legte ihn in Tasse 1. Dieser Vorgang ist ein Spielzug. Nach jedem Zug ist es Voraussetzung, dass die Steine durchmischt werden, damit die Wahrscheinlichkeit gezogen zu werden für alle Steine gleich ist. Die Schülerin hat diesen Vorgang 24 mal wiederholt. Daraufhin befanden sich in Tasse 1 21 rote und 9 blaue Steine. In Tasse 2 befanden sich 21 blaue und 9 rote. Nun wollten wir durch Wahrscheinlichkeitsrechnung ausrechnen, wie groß die Wahrscheinlichkeiten für die drei folgenden Möglichkeiten sind. Die erste Möglichkeit wäre, dass man einen blauen aus Tasse 1 zieht und wiederum einen blauen Stein aus Tasse 2 zieht. Somit hätte ich immer noch jeweils 21 und 9 Steine auf jeder Seite. Die zweite Möglichkeit wäre, dass man einen blauen aus Tasse 1 zieht und einen roten aus Tasse 2. Somit hätte man auf jeder Seite jeweils 22 und 8 Steine. Die letzte Möglichkeit wäre, dass man einen roten aus Tasse 1 zieht und einen blauen aus Tasse 2. Somit hätte man auf jeder Seite jeweils 20 und 10 Spielsteine. Für jede Möglichkeit haben wir die Wahrscheinlichkeit mit dieser Formel ausgerechnet: |
|||||||||||
|
|
|
||||||||||
|
(W (10) = Die Wahrscheinlichkeit für 10 rote/blaue
Steine nach dem nächsten Zug) Ich habe hier nur die Wahrscheinlichkeiten
für acht und zehn Spielsteine aufgeführt, da uns die Wahrscheinlichkeit
für neun Spielsteine in unserem Beispiel nicht weiterbringen würde,
weil sich nichts ändern würde. Zeitmatrix
VV und ZZ ZV VZ |
|||||||||||
|
Grundlage
des philosophischen Gesprächs war: |
|||||||||||

