|
 |
|
|
PROTOKOLL 2. Hj. -3- |
|
| |
|
| HEINRICH-NORDHOFF-GESAMTSCHULE
WOLFSBURG |
KURSPROTOKOLL
|
| MATHE+KUNST
13. Jahrgang GK 2001-02-2 |
Birger
Sechtig & Rainer Randig
|
| 08.01.2002 - 19.03.2002 |
jeweils
7. - 9. Stunde
|
|
|
| Fraktale und Apfelmännchen |
|
Nachdem B. Sechtig bereits Komplexe Zahlen, Chaos und
Fraktale behandelt hatte (als R. Randig nicht anwesend sein konnte),
kam es zum Ende des Semesters darauf an. Mandelbrots Apfel-männchen
aus mathematischer Sicht zu beleuchten. Da B. Sechtig auf einer Philosophen-Tagung
weilte, hatte diese Aufgabe gerechterweise R. Randig zu übernehmen,
zumal der Mathepädagoge schon die Gestaltungsaufgabe zur Goldenen
Spirale gestellt hatte (Protokoll Seite -1-).
Deshalb:
|
Vorbereitung für den 12.03.:
Crashkurs für R. Randig über den mathematischen Hintergrund
der fraktalen Struktur des "Apfelmännchens".
Vorab eine Kurzinformation: "Mandelbrot-Menge [nach dem amerikanisch-französisch-polnischen
Mathematiker B.Mandelbrot, *1924], selbstähnliche fraktale Teilmenge
der komplexen Zahlenebene, die sich durch die Iteratio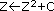n 
erzeugen lässt (C und Z sind komplexe Zahlen). Die Mandelbrot-Menge,
wegen ihrer kugeligen Form auch "Apfelmännchen" genannt,
ist in der fraktalen Geometrie von Bedeutung." ... "Iteration
[lateinisch "Wiederholung"] die, Mathematik: wiederholte Anwendung
desselben Rechenverfahrens auf dabei gewonnene Zwischenwerte, um sich
von einer Näherungs-lösung der exakten Lösung einer Gleichung
anzunähern."
© 2002 Bibliographisches Institut & F. A. Brockhaus
AG |
| Bilder und Anmerkungen |
|
Die labile Weiche (Iteration, s.o.)
|
|
|
| Diese Notizen stehen
auf der linken Tafelseite, leider verdeckt, denn Birger Sechtig macht
mir gerade klar, dass der Mathematiker Leonard Euler (1707-1783) das Symbol
»i« für die Wurzel aus -1 benannt hatte und damit eine
wichtige Entwicklung möglich machte: Carl Friedrich Gauß (1777-1855)
aus Braunschweig spielte als nächster kreativ mit dem Axiom für
imaginäre Zahlen. Gauß konnte nicht ahnen, dass sein Ergebnis,
das System komplexer Zahlen, wiederum die Basis für die Formel von
B. Mandelbrot schuf. Dieser erfand - und auch er wusste tatsächlich
nicht, warum und wie - eine mathematische "Mühle", die,
wenn sie gefüttert wird, ein fraktales System hervorbringt. |
|
Birger Sechtig verdeutlicht den mathematischen Zusammenhang:
|
»Eine solche
"labile Weiche" eignet sich gut zur Einführung in das Verhalten
von Zahlen bei fortgesetzter Iteration.
Sollte ich meinen Anfangswert nur einen "Hauch" weit links von
1 ansiedeln, so streben die entstehenden Zahlen der Null entgegen. Verfehle
ich die 1 als Anfangswert nur um eben diesen "Hauch" nach rechts,
so entwischen mir die Zahlen in Richtung des positiv Unendlichen. Dabei
darf der "Hauch" noch erheblich kleiner sein als man sich gemeinhin
vorstellt.
Wendet man nun eine zugebenermaßen etwas kompliziertere quadratische
Iteration auf die komplexen Zahlen an (s. Tafelbild), so geschieht strukturell
das gleiche , aber natürlich viel komplexer - sie heißen ja
auch komplexe Zahlen.
Die immer wieder neu entstehenden komplexen Zahlen können nun eine
Vielzahl von verschiedenen Verhaltensweisen zeigen. Manche springen ziemlich
chaotisch innerhalb eines endlichen Gebietes umeinander, andere wiederum
bilden spiralarmige oder elliptische bis kreisförmige Galaxien, die
in ihrer Mitte "Schwarze Löcher" besitzen, in deren unmittelbarer
Nachbarschaft sich die Zahlen häufen. D.h. die Zahlen streben diese
an. Die "Schwarzen Löcher" scheinen für die Zahlen
höchst attraktiv zu sein, deshalb nennt man sie auch "Attraktoren".
Natürlich gibt es auch hier das Phänomen, dass die Zahlen ins
Unendliche entwischen. Das vorhin erwähnte endliche Gebiet, das sozusagen
als Gefängnis für die bei der Iteration erzeigten Zahlen dient,
wird in den zugehörigen Abbildungen üblicherweise schwarz gefärbt
und hat den Namen "Mandelbrotmenge". Sie besitzt die berühmte
"Apfelmännchenstruktur".
Leider gibt es kaum Programme, die die Bewegungen der Punkte innerhalb
dieses Gefängnisses dokumentieren (ein Schüler hat ein solches
Programm erstellt und würde es sicherlich eventuellen Interessenten
zur Verfügung stellen.).
Die Komplexität dieser Menge wird deutlich, wenn man sich ihrem Rand
von außen nähert. Bei dem einfachen Einführungsbeispiel
war die Eins sozusagen der ,Fels in der Brandung'. Links ging's gegen
Null, rechts gegen Unendlich. Bei der Mandelbrotmenge gibt es keinen solchen
Felsen. Die Struktur des Randes ist wahrlich seltsam. Wenn ich ihm nahe
auf den Pelz rücke (ihn sozusagen unter die Lupe nehme), entstehen
immer neue kleine Ausbuchtungen, die sog. "Apfelmännchen"
und das hört nie auf. Nehme ich mir z.B. einen dieser Winzlinge aufs
Korn und |
|
|
wähle einen Anfangswert ganz dicht
an seinem Rand, so erscheinen in dieser Vergrößerung eine
Unzahl neuer Apfelmännchen. Das kann ich immer wieder tun, wobei
eine praktische Grenze in der Leistungsfähigkeit meines Rechners
liegt.Die Farben außerhalb der Menge sind der kreativen Gestaltung
des Programmierers zu verdanken. In ihrem Drang zur Unendlichkeit sind
die Zahlen z.B. unterschiedlich schnell und je nach dem, wie eilig sie
es haben, färbt der Programmierer sie unterschiedlich ein. Es gibt
auch noch andere Kriterien, nach denen die Farben gestaltet werden können.
Der optische Eindruck ist somit nicht zwingend vorgegeben sondern Produkt
eines (künstlerischen ?) Gestaltungsaktes.«
|
 |
Die optische Umsetzung der Mandelbrotschen Mühle und ihrer aktuellen
Varianten übt eine starke Faszination aus, unter anderem weil überhaupt
eine rechnerisch-geistige Struktur Form annimmt, weil diese Gestalt nicht
endlich ist, well diese Gestalt Chaos und Ordnung in sich vereinigt, weil
in ihr Abstraktes eine konkrete Form gewinnt. |
Literatur:
Organic art: Spectrum der Wissenschaft, Heft 6/1997: Mathematische Unterhaltungen
Die Fantasiewesen von William Latham. Artikel von Christoph Poppe (s.o.
Link!)
H.-O. Peitgen, P.H. Richter, The Beauty of Fractals.
Images of Complex Dynamical Systems. Springer-Verlag Berlin, Heidelberg
1986
|
|
In Anbetracht der Polivalenz des Kurses und den politisch verursachten
Engheiten unserer pädagogischen Arbeitsbedingungen trutzend hatten
wir unser gemeinsames 4. Kursthema
ZWISCHEN DEN STÜHLEN genannt. Danke, Birger!--
|
| |
|
|
| |
|
|
|
|
| |
